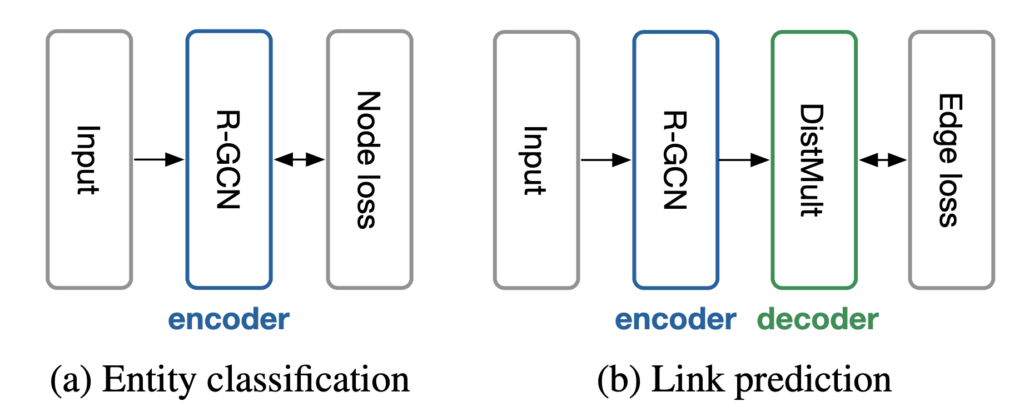
Overview
Knowledge graph embedding (KGE) methods aim at mapping entities and relaions into continuous vector spaces. Specifically, conventioanl KGE methods assign each relation or entity an embedding and train such embeddings using specific loss functions. Compared with them, GNN-based KGE methods usually add a graph neural network (GNN) structure after the embeddings of entities and relations, and such GNN can be used for encoding entities or relations embeddings based on their local neighbor information. The main parts of GNN-based KGEs are designations of GNN layers which indicate how to encode embeddings.
Compared with GNNs on Graphs
In the area of graph representation learning, GNN has been shown to be very effective at accumulating and encoding features from local, structured neighborhoods, and has led to significant improvements in areas such as graph classification and graph-based semi-supervised learning. However, in the area of knowledge graph, the GNN structure should handle relations compared with GNNs on graphs. For example, R-GCN introduce relation-specific transformations which are different from regular GCNs; CompGCN jointly embeds both entities and relations by leveraging a variety of entity-relation composition operations in their GNN structure.
Furthermore, when adapting GNN on knowledge graphs, it usually uses score functions in conventional KGE methods to score the palusibility of triples based on representations ouput from GNNs.
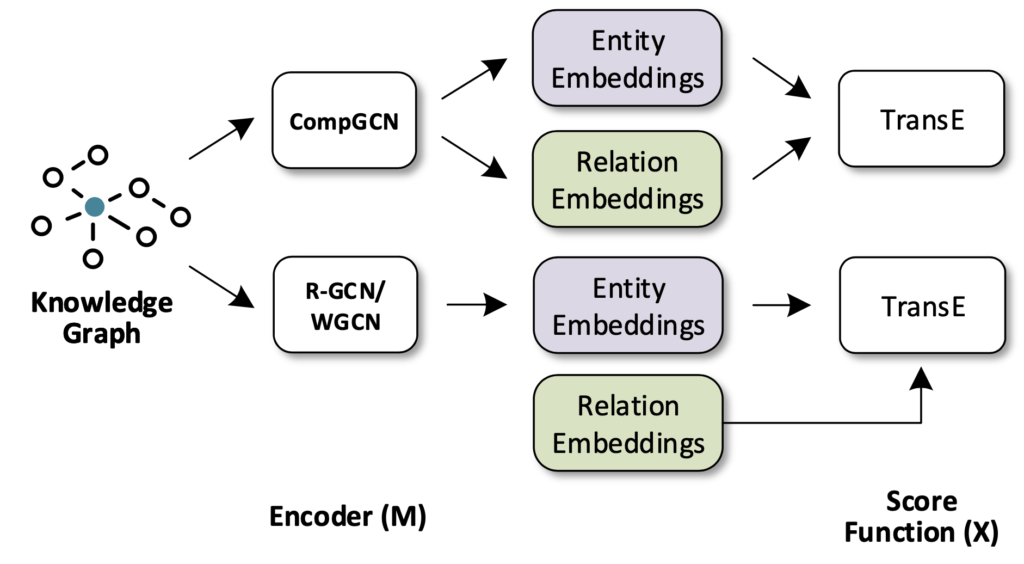
Example: R-GCN
The main part of R-GCN is that how to update entitiy representations during embedding encoding. In R-RGCN, the hidden representation of entities in \( (l+1) \)-th layer in R-GCN can be formulated as the following equation:
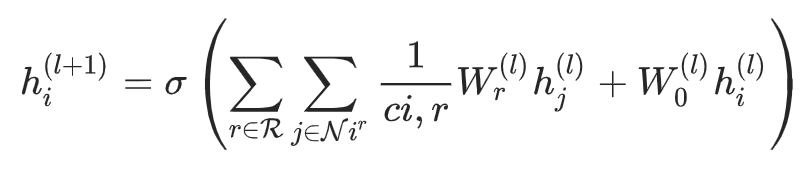
where \( \mathcal{N}{i}^{r} \) denotes the set of neighbor indices of node \(i \) under relation \(r \in R\) and \( c_{i,r} \) is a normalization constant.
After obtainig the output representations of R-GCN, such representations can be used for calculating loss functions based on different tasks.