C-KGEs

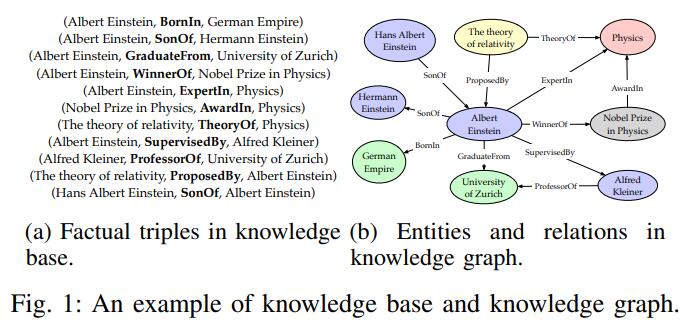
NeuralKG reproduces the conventional knowledge graph embedding models, namely C-KGEs, which are designed to map entities and relations in the knowledge graph to a specific vector space and score the truthfulness of the triples using a designed scoring function, resulting in a high-quality vector representation of entities and relations.

This part introduces C-KGEs in terms of a representation space, scoring functions, and some specific model examples.

Representation Space

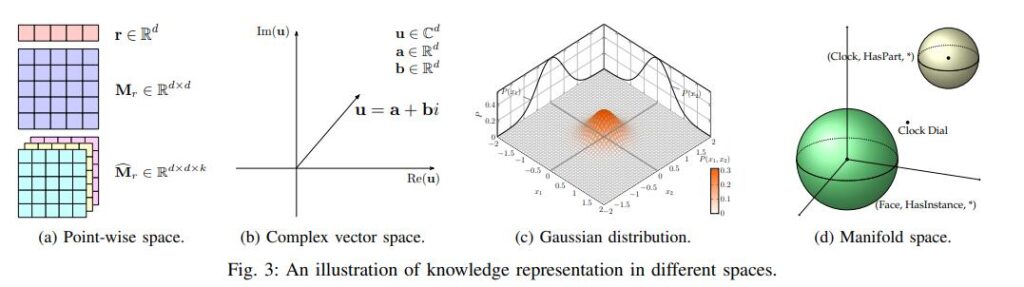
The key issue in knowledge graph representation learning is the low-dimensional distributed embedding space of learning entities and relations. The main representation spaces currently used are point-wise space, complex vector space, Gaussian space, manifold. The representation space should be subject to three conditions, namely the differentiability, computational possibility and definability of the scoring function under the assumptions of that space.

Point-Wise Space：This space is the most used spatial assumption, as shown in Figure a below, where entities are represented as points in a space and relationships are mapped as vectors or matrices. translation models such as TransE use this representation space.
Complex Vector Space：As shown in figure b below, unlike the real-valued space, the entity representation in the complex space consists of real and imaginary parts. The representative models are ComplE, RotatE.
Gaussian Space：As shown in Figure c below, there is also work that uses Gaussian space to represent uncertainty in entities and relationships, represented by KG2E and TransG.
Manifold and Group: As shown in Figure d below, the knowledge representation for point-wise modelling is an unsuitable algebraic system and too strict a geometric form. Several researchers have begun to investigate knowledge representation in manifold spaces, Lie groups, and dihedral groups. Representative works include MainfoldE, TorusE and DihEdral.

Scoring Function

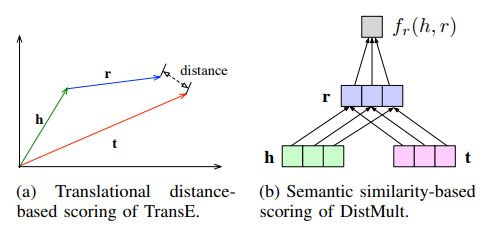
Scoring functions are used to measure the truthfulness of fact triples and are also referred to as energy functions in energy-based learning frameworks. There are two typical types of scoring functions, distance-based and similarity-based scoring functions.

Distance-based Scoring Function：The distance-based score function measures the truthfulness of a fact triple by calculating the Euclidean distance between the head and tail entities, with closer distances representing more credible samples.
Similarity-based Scoring Function：The semantic similarity-based scoring method measures the plausibility of a fact triple by semantic matching, which is usually done using a multiplicative matrix formula.

The following figure shows the scoring functions based on distance and semantic similarity using TransE and DistMult respectively

Model Examples

TransE

This is one of the earliest approaches to knowledge graph embedding. The authors were motivated by the word2vec model, which found an interesting translation invariance in the word vector space, and treated the relationships in the knowledge graph as some kind of translation vectors between entities.

Distance-based scoring function:

f_r(h, t) = |l_h + l_r - l_t|_{L1/L2}

In the actual learning process, in order to enhance the differentiation of the knowledge representation capability, TransE uses the maximum interval approach and defines the following optimisation objective function:

L = \sum{(h,r,t)\in S}\sum{(h^\prime,r^\prime,t^\prime)\in S^-}max(0, f_r(h,t) + \gamma - f_{r^\prime}(h^\prime, t^\prime))

where is the set of correct triples, is the set of incorrect triples, max(x, y) returns the larger of x and y, and is the interval distance between the scores of the correct triples and the incorrect triples. The incorrect triple is obtained by randomly replacing the head entity or the tail entity. The following diagram shows the training process of TransE：

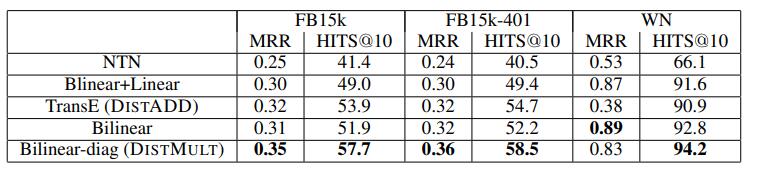
Although TransE is simple and effective, it has the drawbacks of not being able to handle 1-N, N-1, N-N relations and not being able to handle symmetric relations. Therefore, a large amount of research work has been done since then to extend and apply TransE.

DistMult

DistMult is a classical semantic matching model based on a similarity scoring function. The model measures the likelihood of triple facts to hold by matching the potential semantics of entities and relations in the embedding vector space. DistMult is a further simplification of RESCAL, which represents entities by vectors and relations by diagonal matrices. Its scoring function is

𝑓(ℎ,𝑟,𝑡)=𝐡^T diag(𝐫)𝐭

References

[1] A Survey on Knowledge Graphs:Representation, Acquisition and Applications.